Widerstand und Leitwert

Nach dem Schaltplan wird ein Stromkreis, in dem eine Glühlampe, eine Spule und ein Strommesser hintereinander geschaltet sind, an eine Spannungsquelle gelegt. Nimmt man je einen der beiden Verbraucher aus dem Stromkreis heraus, so zeigt der Strommesser jedes Mal einen stärkeren Strom an, wird der Verbraucher wieder in den Stromkreis eingeschaltet, so sinkt die Stromstärke.

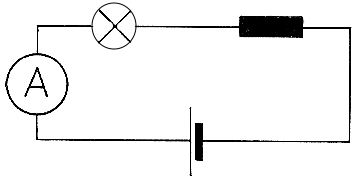
Jeder Verbraucher hat also die Eigenschaft, den Strom im Stromkreis zu schwächen, ihm einen Widerstand zu bieten. Man kennzeichnet also mit dem Begriff Widerstand eine Leitereigenschaft, die das Verhalten des Verbrauchers gegenüber deren Stromdurchgang zeigt.

Die Stromstärke in einem Stromkreis ist demnach außer von der Spannung, die den Strom verursacht, auch von dem Widerstand des Leiterkreises abhängig. Es besteht also eine Beziehung zwischen der Spannung U, der Stromstärke I und dem Widerstand R des Stromkreises.

Zusammenhang zwischen Spannung und Stromstärke

Nach dem Schaltplan im Bild wird an einen Verbraucher R eine regelbare Spannung gelegt. Die Stromstärke I im Stromkreis wird durch den Strommesser A, die Spannung U am Verbraucher durch den Spannungsmesser V angezeigt. Die einander zugeordneten Werte von Spannung und Stromstärke Sind in der folgenden Tabelle eingetragen.

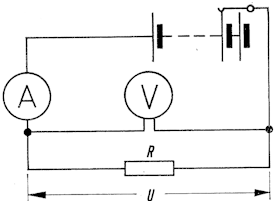
\(U\; \text{in}\; V\)	\(I\;\text{in}\;A\)	\(\displaystyle \frac{U}{I}=R\; \text{in}\;\frac{V}{A}\)
\(2\)	\(0,025\)	\(\displaystyle \frac{2}{0,025}=80\)
\(4\)	\(0,05\)	\(\displaystyle \frac{4}{0,050}=80\)
\(6\)	\(0,075\)	\(\displaystyle \frac{6}{0,075}=80\)
\(8\)	\(0,100\)	\(\displaystyle \frac{8}{0,100}=80\)
\(10\)	\(0,125\)	\(\displaystyle \frac{10}{0,125}=80\)

Der in der Tabelle in Spalte 3 gebildete Quotient \(\displaystyle\frac{U}{I}\) aus Spannung und Stromstärke hat für den untersuchten Verbraucher einen konstanten Wert R. Ersetzt man im Versuch den Verbraucher durch andere Verbraucher, so erhält man andere Werte für die Stromstärken. Für das Verhältnis \(\displaystyle\frac{U}{I}\) ergeben sich aber in jedem Fall wieder konstante, für die einzelnen Verbraucher charakteristische Werte.

Definition des elektrischen Widerstandes

Aus dem Begriff des Widerstandes folgt, dass von zwei Verbrauchern demjenigen ein größerer Widerstand zuzuschreiben ist, der bei gleicher Stromaufnahme in beiden Verbrauchern eine höhere Spannung erfordert bzw. der bei gleicher Spannung an beiden Verbrauchern einen geringeren Strom aufnimmt. Wie der Widerstand eines Verbrauchers, ist auch der für ihn charakteristische konstante Quotient \(\displaystyle R=\frac{U}{I}\) größer, wenn entweder bei gleicher Stromstärke I die Spannung U größer ist, bzw. wenn gleicher Spannung U die Stromstärke I kleiner ist.

Man definiert deshalb :

\(\displaystyle \text{Widerstand des Verbrauchers}=\frac{\text{Spannung am Verbraucher}}{\text{Stromstärke im Verbraucher}}\)

Der in der Tabelle oben in Spalte 3 gebildete Quotient \(\displaystyle \frac{U}{I}\) gibt somit den Widerstand des Verbrauchers an.

Maßeinheit des Widerstandes

Auf Grund internationaler Vereinbarung wurde das Ohm (Kurzzeichen Ω) als Widerstandseinheit eingeführt.

Historisch

1 Ω wird technisch dargestellt durch den Widerstand einer Quecksilbersäule von der Temperatur des schmelzenden Eises, deren Länge bei durchweg gleichem Querschnitt von 1 mm2 106,3 cm und deren Masse 14,4521 g beträgt.

Zur technischen Darstellung der Widerstandseinheit wurde Quecksilber gewählt, weil es als Flüssigkeit von gleichmäßiger Beschaffenheit ist und durch Destillieren vollkommen rein verwendbar ist.

Nach der Definitionsgleichung des Widerstandes \(\displaystyle \frac{U}{I}\) wird \(R =l \;Ω \) wenn \(U = 1\; V \) und \(I = 1\; A\) ist, d. h. , ein Verbraucher hat den Widerstand 1 Ω , wenn in ihm bei einer Spannung von 1 V ein Strom von 1 A fließt. Zwischen den Einheiten des Widerstandes, der Spannung und der Stromstärke besteht die Einheitengleichung :

\(\displaystyle 1\;Ω=\frac{1\;V}{1\;A}\)

Der Leitwert

Je größer der elektrische Widerstand eines Verbrauchers ist, desto geringer ist seine Fähigkeit, den Strom zu leiten und umgekehrt. Diese Fähigkeit wird Leitwert genannt (Formelzeichen G). Der Leitwert ist der Kehrwert des Widerstandes :

\(\displaystyle Leitwert=\frac{1}{Widerstand}\;\;\;\;\;\;\;\; G\frac{1}{R}\)

\(\displaystyle Widerstand =\frac{1}{Leitwert}\;\;\;\;\;\;\;\; R\frac{1}{G}\)

Die Einheit des Leitwertes ist das Siemens (Kurzzeichen S). Zwischenden Einheiten des Leitwertes und des Widerstandes bestehen somit die Einheitengleichungen :

\(\displaystyle 1\;S=\frac{1}{1\;Ω} \;\;bzw.\;\;1\;Ω=\frac{1}{1\;S} \)